he search for more effective and less toxic therapies for cancer has rightfully focused on the discovery and development of medications that challenge the viability of cancer cells. But in addition to finding the drugs themselves, it is critical to define their best applications, which should include considerations of dose level and schedule. In this regard, there is much to gain from studying the growth kinetic behavior of cancerous masses over time. It has proven to have immediate applications, especially in the design of the most effective adjuvant chemotherapy regimen for primary breast cancer. It is also one that may well be relevant to one of the most stimulating innovations in contemporary cancer therapy: antibody-drug conjugates, which will be discussed in a later essay.

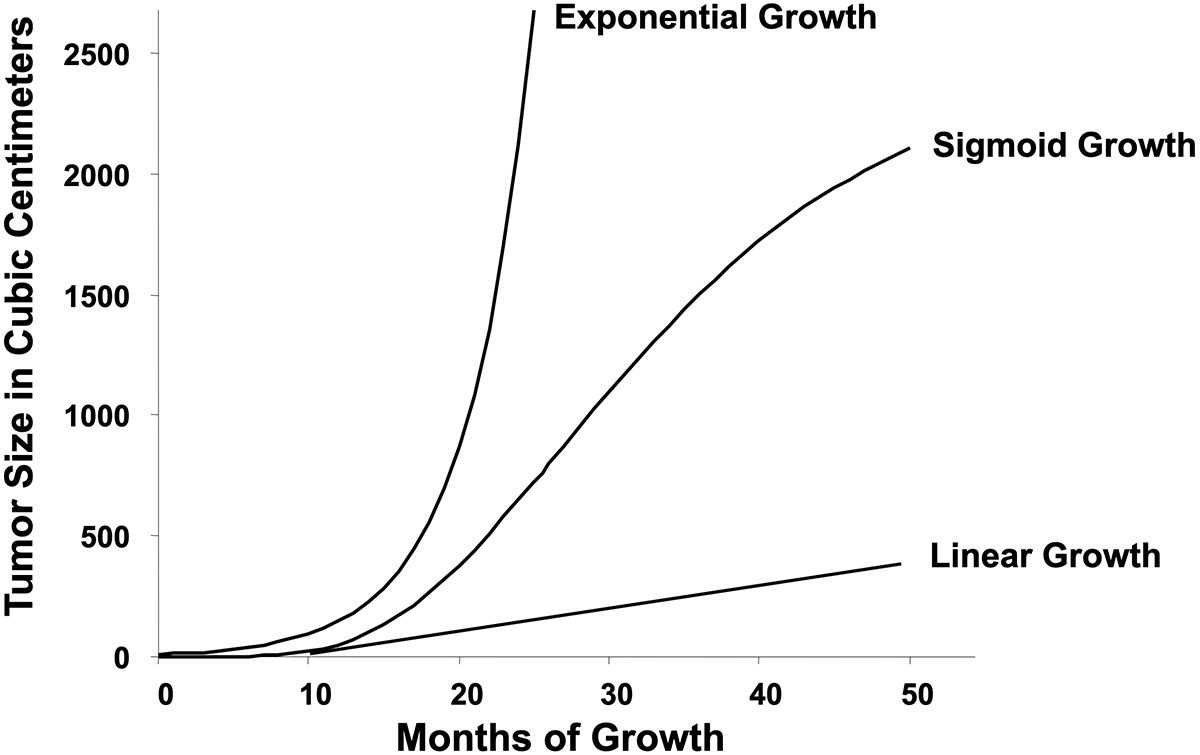
Two of the most influential papers in the philosophy of cancer are Hanahan and Weinberg’s description of its so-called hallmarks. This seminal body of work provides a roadmap for conceptual advances including the definition of drug targets. But while its list of features is close to comprehensive, it does omit the fact that cancers universally follow a pattern of growth called sigmoid. Sigmoid growth cannot, as discussed in a follow-up essay, be the simple consequence of cancer cell autonomy. This observation is key to a better understanding of cancer with practical implications.

Among the infinite number of possible sigmoid curves, the one described by Benjamin Gompertz in 1825 is most used in oncology. Its point of maximum growth rate (and point of inflection) is at about a third of the theoretical plateau size. In fact, however, there is considerable variability in the shape of sigmoid curves in nature, and the inflection point may be higher or lower than one-third of plateau size. Nevertheless, a consistent finding is that the parameters of the Gompertzian equation are highly correlated, meaning that tumors that initially grow most quickly tend toward a plateau size smaller than those that initially grow more slowly. First shown in 1976, this observation was then extended to many model systems. The implications of this discovery will be discussed in a subsequent essay.

The Skipper-Schabel and Goldie-Coldman Models

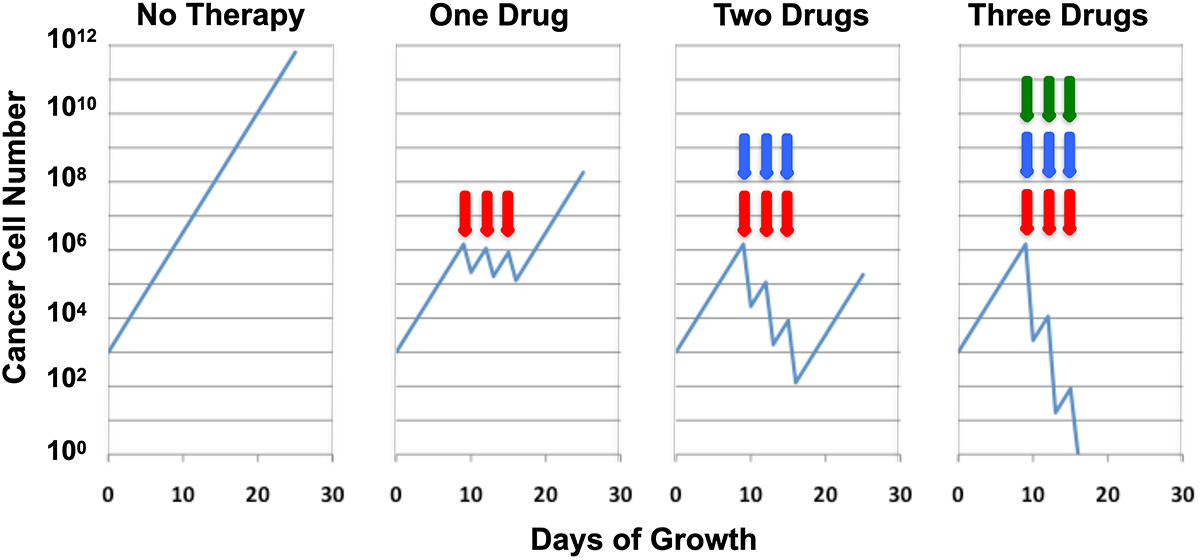
An experimental observation published in 1977 brought sigmoid growth kinetics out of the conceptual space into the arena of practical therapeutic applications. Howard Skipper and colleagues, funded by the National Cancer Institute under Vincent DeVita, revolutionized cancer therapeutics in the 1960s by establishing principles of chemotherapy that are still influential today. The basis for their thinking was the observation that a given administration of chemotherapy killed a specific fraction of the cancer cells present rather than an absolute number. Since a fraction could be quantified logarithmically, their work has been termed the log-kill model. (For example, a reduction of one logarithm to the base 10 is a 90% reduction in cell number.) The principles they developed included using the highest possible dose level to achieve optimal results, using drugs as early in the tumor growth history as possible, and using many drugs simultaneously (Figure 1). Their laboratory success created a wave of enthusiasm among cancer physicians, partially justified because there has been clear value in the application of these principles. These include historical events such as the cure of Hodgkin’s disease, the development of perioperative chemotherapy, and the entirety of combination chemotherapy.

However, the main experimental model they used, murine leukemia L1210, grows exponentially and is very responsive to chemotherapy, two features not wholly applicable to human disease. Perhaps for this reason, some predictions of the work have been disappointing. Examples are the failure of high-dose chemotherapy with autologous bone-marrow transplantation for breast cancer and, in general, the lack of universal cure via adjuvant polychemotherapy.

Two overlapping but distinct conceptual models that sought to address these matters were actively debated in the 1980s. James Goldie and Andrew Coldman suggested that the problem was the rapid emergence of drug resistance by spontaneous—rather than induced—mutation, which is reminiscent of the Luria-Delbrück experiment. The logical conclusion of their thinking was that it would be best to introduce as many active drugs as possible as early as possible in a treatment plan. Any delay, they reasoned, would allow time for resistant clones to arise. Should multidrug combinations prove impossible to administer near-simultaneously, they advocated splitting them into two combinations and using those in strict alternation.

The Norton-Simon Model

Larry Norton and Richard Simon focused instead on the application of log-kill theory, born from experiments using an exponentially growing tumor, to tumors following sigmoid growth curves. They discovered that the log-kill model worked in Skipper’s experiments because in exponential growth the growth rate relative to population size is always the same. If an L1210 leukemia increases in size by 50% in a few days when it is small, it would increase by 50% over the same time interval after it grew to be larger. Because the fractional gain per unit of time in exponential growth does not vary, the fractional kill also does not vary with population size. However, in sigmoid growth the growth rate is always changing. Norton and Simon found that in these situations the fractional kill is also not constant but rather proportional to the relative growth rate. Hence, small sigmoid cancers with higher relative growth rates should experience greater cell-kill than were the same tumor treated with the same therapy at a larger size when its relative growth rate would be smaller.

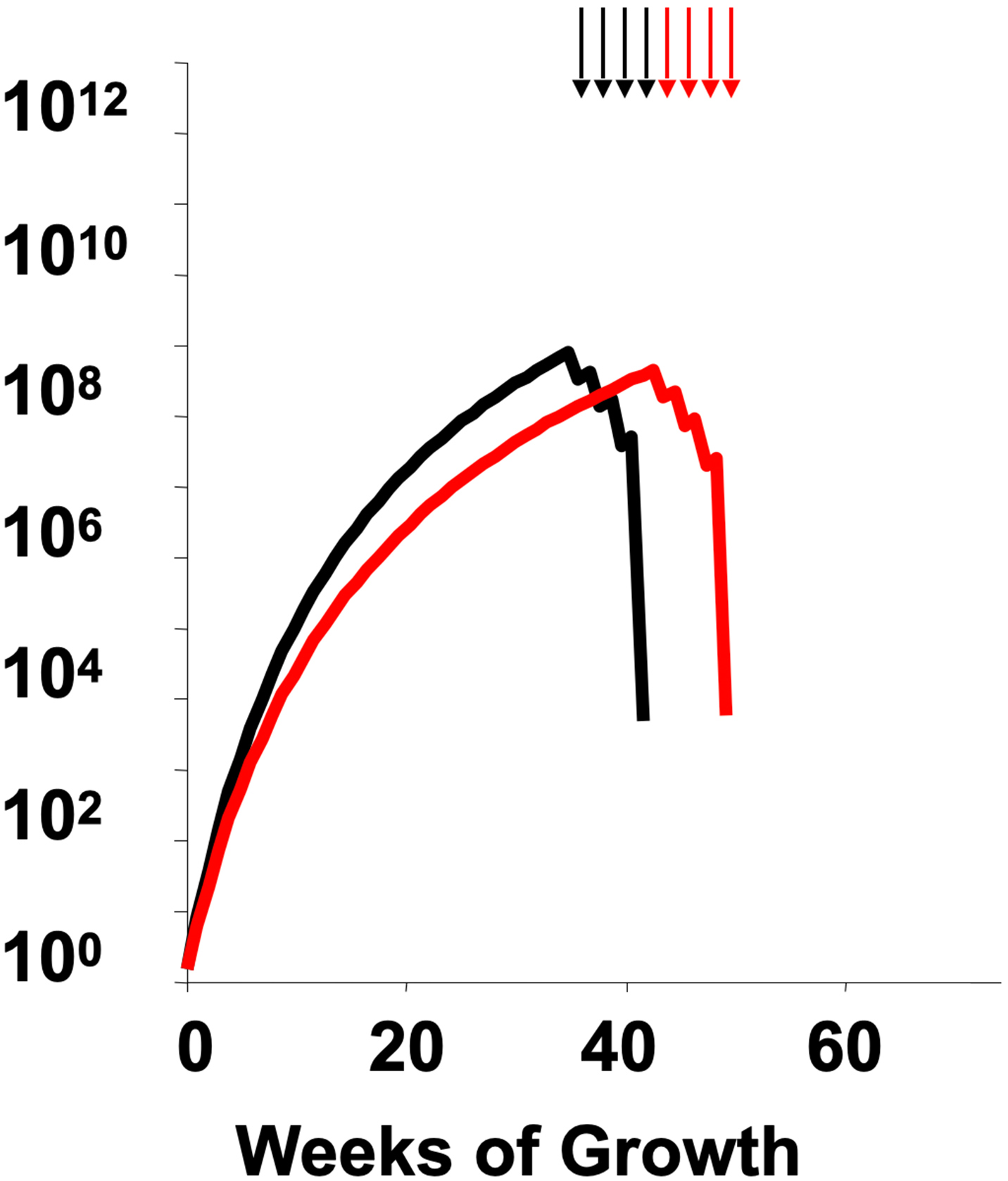
This so-called Norton-Simon hypothesis has been successfully applied to cancer therapeutics. Since optimal killing of cells is critical for optimal results, the model asserts that this could be achieved by three scheduling innovations (Figure 2). The first respects dose-response relationships, but not in the sense of promoting dose-level escalation but rather to avoid unnecessary dose-level reduction. The idea is to use combinations only when the dose level of each component does not have to be compromised below an effective level to avoid excessive toxicity.

This approach, of course, could force a limit to the number of drugs in the combination, which would be a problem when cellular heterogeneity in drug sensitivity is encountered. The solution, then, is to use combinations, constructed using the first principle, sequentially, a full course of one followed by a full course of the other, rather than in strict alternation. This is in contrast with the Goldie and Coldman approach of strict alternation, an important but often subtle distinction.

The third innovation is to minimize the time between applications of therapy by shortening intertreatment intervals. This would allow the application of a subsequent cycle of treatment at as small a tumor size as possible after the previous cycle. The development of granulocyte colony stimulating factors is what made the application of the third principle, a manipulation often called dose density, practical. Dose density is distinguished from the use of higher dose levels, although both approaches have been termed dose intensification. It should be noted that sequential therapy is also a form of dose density in that the Goldie-Coldman idea of strict alternation dilutes each combination over time, spreading out the number of cycles over a longer time period.

Experimental Validation of Norton-Simon

Two early clinical trials are notable in this regard, both in the post-operative therapy of primary breast cancer, a setting chosen to apply the second of Skipper’s principles to treat at a small tumor size. The first is a trial by Gianni Bonadonna and colleagues that pitted alternating regimens for breast cancer (CMF and doxorubicin) vs. using a full course of one followed by a full course of the other. The sequential approach, as predicted by the Norton-Simon hypothesis, turned out to be superior. The second is CALGB 9741, led by Marc Citron. This built upon an earlier trial by Craig Henderson and colleagues that established the value of adding sequential paclitaxel to the then-standard combination of doxorubicin and cyclophosphamide (Figure 3). CALGB 9741 discovered that using two-week intertreatment intervals, i.e., dose density, significantly improved results over the then-conventional three-week intervals. Moreover, this effect was found even when the adjuvant chemotherapy was split into single-agent doxorubicin followed by single-agent paclitaxel, followed by single-agent cyclophosphamide—a result further challenging the requirement of simultaneity in combination chemotherapy. These results spawned more than two dozen subsequent trials, involving more than 37,000 volunteer patients, which, when analyzed in overview, clearly confirm the principles of the Norton-Simon hypothesis.

It is thus well established that sigmoid growth has tangible clinical implications. But these go beyond the design of optimal dose schedules of conventional cytotoxic drugs: the application of these principles to novel therapeutics, especially the antibody-drug conjugates, is a topic to be discussed in a subsequent essay.